PersistentHashMap, Part 1 -- Making a hash of things

The first of several posts on implementing immutable, persistent Hash Array Mapped Tries. This post describes the data structure at a high level; subsequent posts will provide F# code for the base implementation and then discuss transiency.

• Part 1: Making a hash of things (this post)
• Part 2: The root
• Part 3: The guts
• Part 4: Other matters
• Part 5: At a loss

Making a hash of things

The most complex data structure in the Clojure catalog has to be clojure.lang.PersistentHashMap. This is Phil Bagwell’s Hash Array Mapped Trie (HAMT) as modified by Rich Hickey to be immutable and persistent. (Bagwell’s original paper is available here)

We want to build maps taking associating keys (of arbitrary type) with their corresponding values. We are interested in the following operations:

• assoc – add a key/value pair to the map
• without – remove a key’s entry from the map
• find – find the value associated with a key

(The full gamut of basic operation on maps in the Clojure ecosystem is larger. These three are definitional; most of the rest involve iterating over the key/value pairs in the map and performing various operations on them.)

Because we are living in the land of the persistent and immutable, the general case for the assoc and without operations is to generate a new map with the desired change. The original map is left unchanged. (The find operation is a read-only operation and does not change the map.) For efficiency, we will need the new map to share as much structure are possible with the original map.

HAMTs can viewed a mash-up of simple hash tables, binary search trees and the ideas we covered when discussing persistent bit-partitioned vector tries (see Persistent vectors, Part 2 – Immutability and persistence).

Let’s look at some candidates structures.

Simple hash tables

The theory on hash tables of this type is extensive; you can get started here.
The simplest hash table uses an array to store the values in the map. A hash function is applied to a key to determine the location at which to store its value. The hash function should produce a good distribution of hash codes across the range of possible keys. The hash function might produce arbitrary integers; we mod the hash code to the size of the array to produce the index.

One has to deal with the two keys hashing to the same index, i.e. key collision. Many techniques have been proposed. Look at the article.

Simple hash tables are not designed for immutability. One would need to copy the entire array on each key/value change. You could contemplate using something like PersistentVector for the array storage. But … don’t. There are trade-offs in the the size of the PersistentVector as you start off, the need to grow it (which, given how modding comes in, requires recomputing indexes and moving all the elements to new positiions, which means lots of copying), and on and on. It’s just not going to work.

Tree indexing

Rather than modding in integer-valued hash code to a small-ish range in order to index into an array, we could try to use the entire key value.
This approach uses trees instead of arrays. As an example, we could store key/value pairs in a binary tree. Treating the hash code as a sequence of bits and mapping 1 to Left and 0 to Right, the hash code of an item describes a path through the tree. One does not need to use all the bits, just enough to distinguish a given key from all the others. Assuming 5-bit hashcodes, this picture illustrates how a given set of four keys would be distributed.

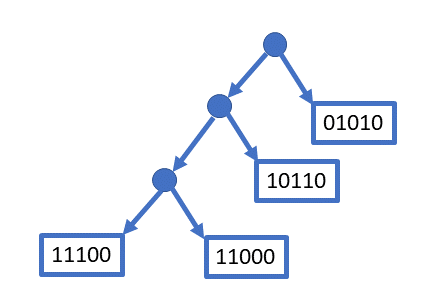
Again, one must deal with collisions.

There are some problems to deal with. The tree can become unbalanced, leading to some branches being very long. This affects retrieval and copying performance. There are a variety of ways of managing the tree structure to promote balance. One can use a self-balancing tree structure such as an AVL tree or a red-black tree. (In fact, a persistent implementation of red-black trees is the underlying structure for PersistentTreeMap, used when entries need to be kept in sorted order.)

Even with balancing, a binary branching structure leads to poor memory management. Many nodes must be accessed along the path determined by the key. These nodes are going to scattered in memory, leading to lots of memory accesses and poor cache performance. One can address this by chunking the tree into arrays.

PersistentVector

The PersistentVector class solves some of these problems. Its chief feature is using multi-way branching at each node to improve memory-access efficiency. PersistenVector is a kind of map; an index into the vector is a key. The mechanism of tree traversal in PV shows how we can use chunks of the integer to determine branching. There are two differences from the general mapping situation: (1) we are restricted to integer keys in a contiguous range, (2) there are lots of empty positions in the vector.

A good approach would be to use the mechanisms of multi-way branching from PV, remove the restriction on key values, and deal with the sparseness of the keys.

Hash Array Mapped Trees

And this leads us to the hash array mapped trie/tree (HAMT). Nodes have a (small-power-of-two)-way branching factor. The branch to choose at a particular level is based on several contiguous bits in the hash. Which bits depend on the branching factor (power of two) and the level in the tree. Using four as the branching factor, we might see a configuration such as the following:

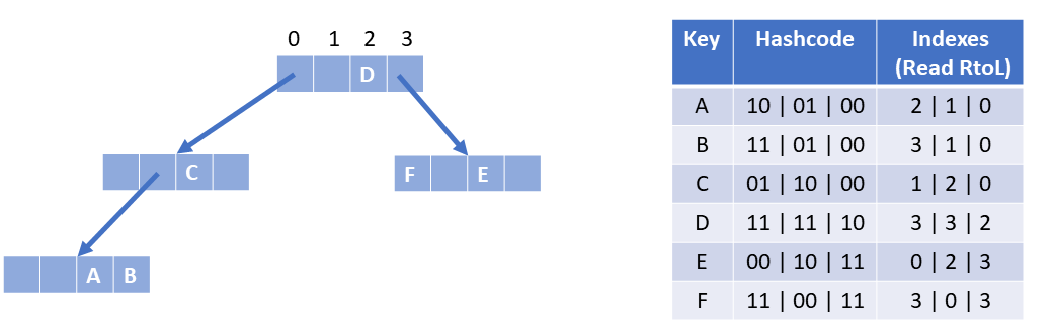
In the PersistentVector structure, indexes are contiguous; there are no gaps. With HAMTs, there can be considerable sparseness. We have to deal with the gaps. In the process of doing so, we can gain several efficiencies.

First, we absolutely must detect a gap – that a given hash code has no entry. We can do this by not having a branch out of an index node. But this can lead to a lot of wasted space in the array in the node. We can compactify the array, providing entries only for occupied cells. But now given the index, we must first determine if it is occupied and then, if occupied, determine what index in the compacted array it maps to. This is done with a bitmap and a bit of bit manipulation.

We will allocate array storage only for the occupied cells. The node will have a bitmap telling us which cells would be occupied in the full array. Then we use a neat trick to map an index to the array cell holding its value; this trick involves calculating the number of one bits (sometimes known as the population count) in a masked section of the bitmap. (See below.)

One last efficiency hack. In a given node’s array, we can store key/value pair and/or links to the index the next level down. This way we need only go down the tree as far as necessary to find the key/value pair. This is a form of path compression.

Here’s a rough sketch. Let’s assume a branching factor of 32 (a common choice). Five bits can be used to provide an index in the range [0,31]. We begin with the rightmost five bits to compute the index to check. At the next level, we take the second five bits, etc. (We did the same thing in PersistentVector.) Say we are two levels down from the root, and supposed the hash for our key is 0xDD707. (I’ll ignore the zeros on the most significant end.) Then we need to extract the third set of five bits. From this picture

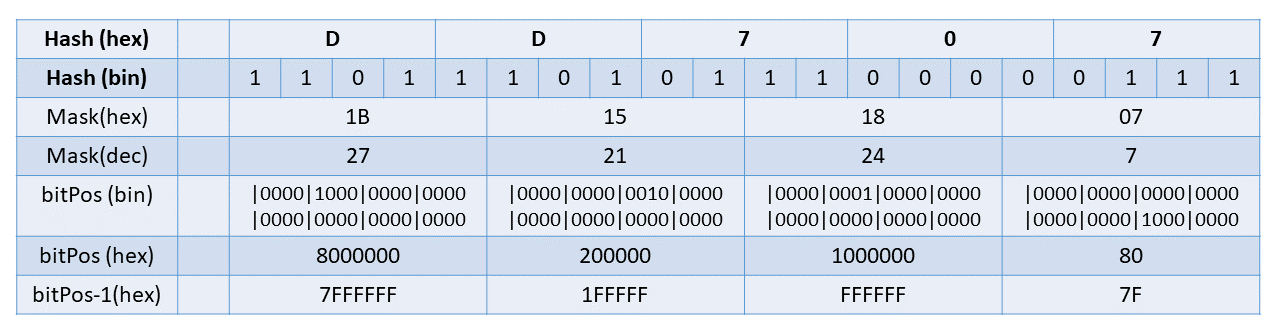
we compute an index of 21. If we were not working with compacted array storage, we would just look at entries[21] for the node in question and see if it represented a key/value pair, a link to another node one level down, or was empty. However, if we are using compacted array storage, we must figure out where index 21 is mapped to. Of course, it might be that index 21 is empty and hence not in the array. We check that by seeing if bit 21 is set in the node’s bitmap. If not, then the key is not present.

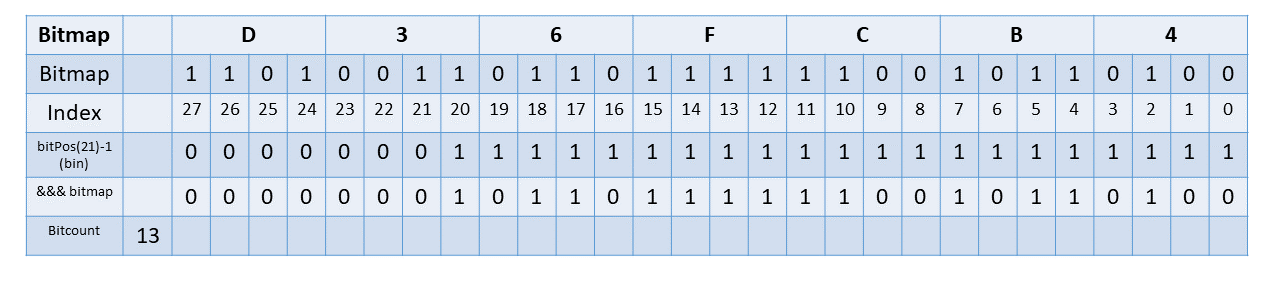
Suppose the node in question has bitmap 0xD36FCB4. It is set in bits 2, 4, 5, 7, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21, 24, 27. So index 21 is indeed occupied in this node’s array.
But mapped to what index in the node’s array? Well, you can count how many bits prior to 21 are set. That is 13 in this case. So to find intended index 21 we look in index 13 in the compacted array.

Top-level code

These calculations are fairly easy to capture in code. (And you will see almost identical code in PersistentVector.) First we must extract five bits from the appropriate place in the hash. mask does that – the shift will be five times the level in the tree.

    let mask (hash, shift) = (hash >>> shift) &&& 0x01f

We now need an integer with the appropriate bit set (in our example, 21):

    let bitPos (hash, shift) = 1 <<< mask (hash, shift)

The text for whether our index is present in the compacted array is

        let bit = bitPos (hash, shift)

        if bit &&& bitmap = 0 then  
            // not in the array
        else
            // in the array

If the key is indeed, present, we need to know how many bits are set below it. The trick is to take our bit and subtract one. That will give us all ones in the positions prior to us (0 to 20) If we AND that mask with the bitmap for the node and then count how many bits are set in the result, we will have our index. This function will do the trick:

    let bitIndex (bitmap, bit) = bitCount (bitmap &&& (bit - 1))

The function bitCount is sometimes referred to as the population count. Here is an implementation:

    let bitCount (x) =
        let x = x - ((x >>> 1) &&& 0x55555555)
        let x = (((x >>> 2) &&& 0x33333333) + (x &&& 0x33333333))
        let x = (((x >>> 4) + x) &&& 0x0f0f0f0f)
        (x * 0x01010101) >>> 24

(You can find all kinds of variations on this code. )

The code for bitCount can be found in a lot of places. (Look online. Or get a copy of Hacker’s Delight by Henry S. Warren, Jr. It’s a fun book.) Some CPU architectures have a single instruction which computes this. You may have access to a function that inlines to that instruction (e.g., System.Numerics.BitOperations.PopCount).

Adding persistence and immutablility

There are plenty of tutorials available online with wonderful pictures and animations that illustrate the ideas behind persistent, immutable tree structures. I refer you to them for nice visuals. Here, I’ll provide some mediocre visuals to tell our story. It is much the same story as in PersistentVector. I’ll retell it here anyway.

In immutable collections, operations that modify the collection, such as an insertion or a deletion do not modify the data structure. Say we have a tree-shaped data structure and we are doing an insertion into the tree. We will make a copy of the tree with the new item inserted, leaving the original tree intact. We can do this reasonably efficienty if we are clever enough to have our new tree share as much structure of the old tree as possible, the parts that don’t need to change. This is safe if the starting tree is immutable because the parts from the original tree are guaranteed not to change. Consider the following binary tree. Nodes are labeled with id:datum.

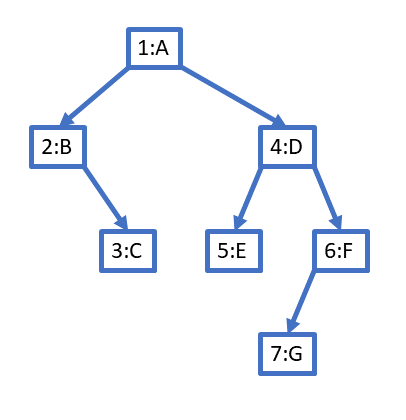
If we want to modify the data of node 6 to be Q, we must make copies of all nodes from 6 back to the root (thus, nodes 4 and 1). They point to the nodes in the original tree when possible and to the new nodes where required to create the correct structure with a minimum of duplication:

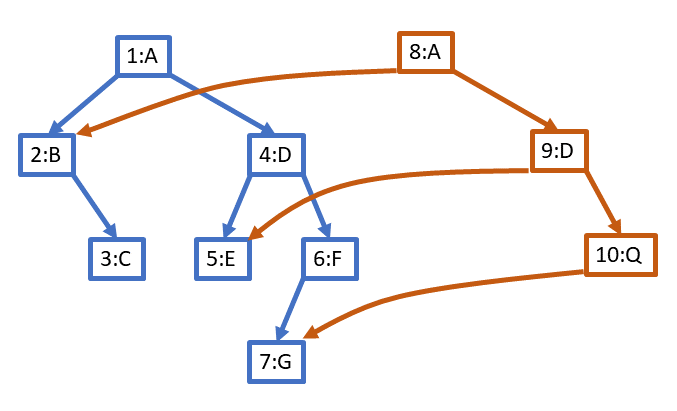
For clarity, here is the new tree standing alone.

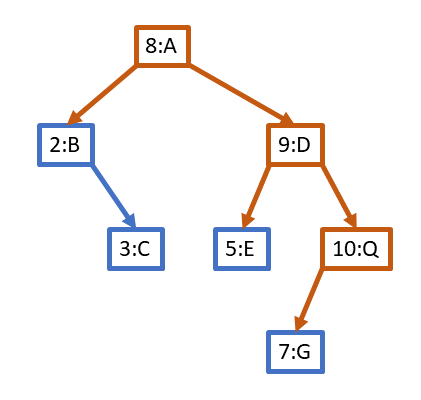
The original tree still exists, unmodified. Copying and resuse are the secrets to immutability, persistence, and efficiency.

And now we can code. In the next post, I’ll cover the basics of an implementation of PersistentHashMap in F#.