For your Cons-ideration
To build a Lisp, you could perhaps start with the simplest data structure, the cons cell: a simple record structure with two fields that hold pointers and a staple of Lisp implementation from the beginning.
Clojure likes immutability, so we don’t even need setters for the fields.
type Cons = {Car:obj; Cdr:obj}
(In old Lisps, car and cdr were the traditional names for the fields we now might call first and rest. And they would be mutable.)
Okay. Good. We’re done.
Well, not really. A Cons in Clojure has to slot into the ecosystem that Clojure defines. Cons cells define a sequence, which means they have to support iteration through a sequence in the manner Clojure requires. In Clojure, a cons cell can have metadata attached. And so on.
If you diagram the inheritance relationships of the various interfaces and concrete collection classes in Clojure, you get a picture something like this:
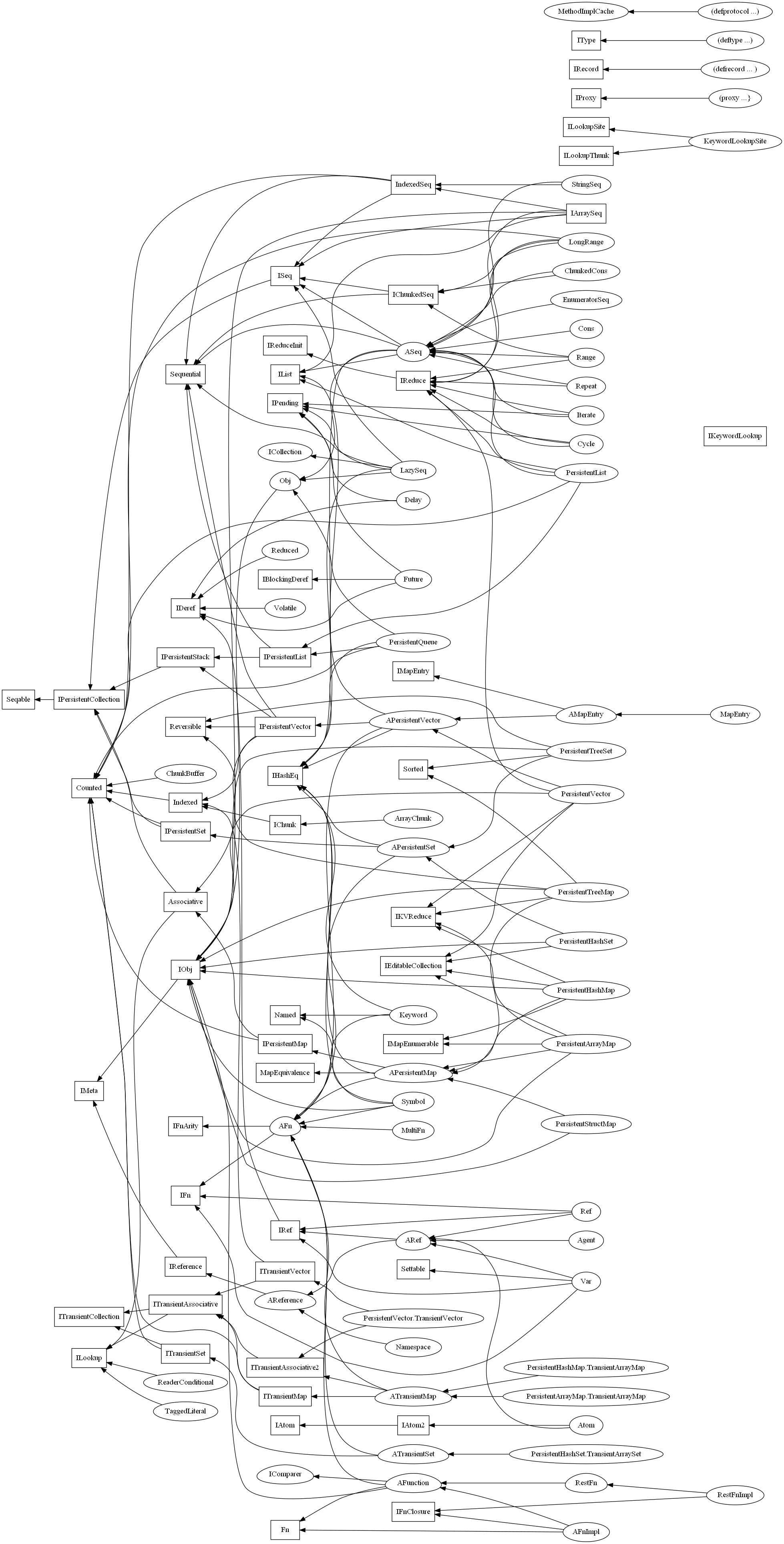
(And at least one interface has been added since I originally drew this.)
It does not matter if you cannot read all the names. Just soak it in.
And this only shows the direct inheritance relationships. It does not show, for example that Seqable has a method with a return type of ISeq, thus creating a circularity.
F# does not like circularities. Neither does my brain when it is trying to figure out how things fit together and how to get started on an implementation.
What is the minimum needed to implement Cons? Let’s grab the tree by the Cons, pull it up, and see what comes up with it. In the following graph boxes indicate interfaces, ‘eggs’ indicate abstract classes, and ellipses indicate concrete classes. Solid lines indicate inheritance; dashed lines indicate a reference in the API of the ‘tail’ to the ‘head’ type.
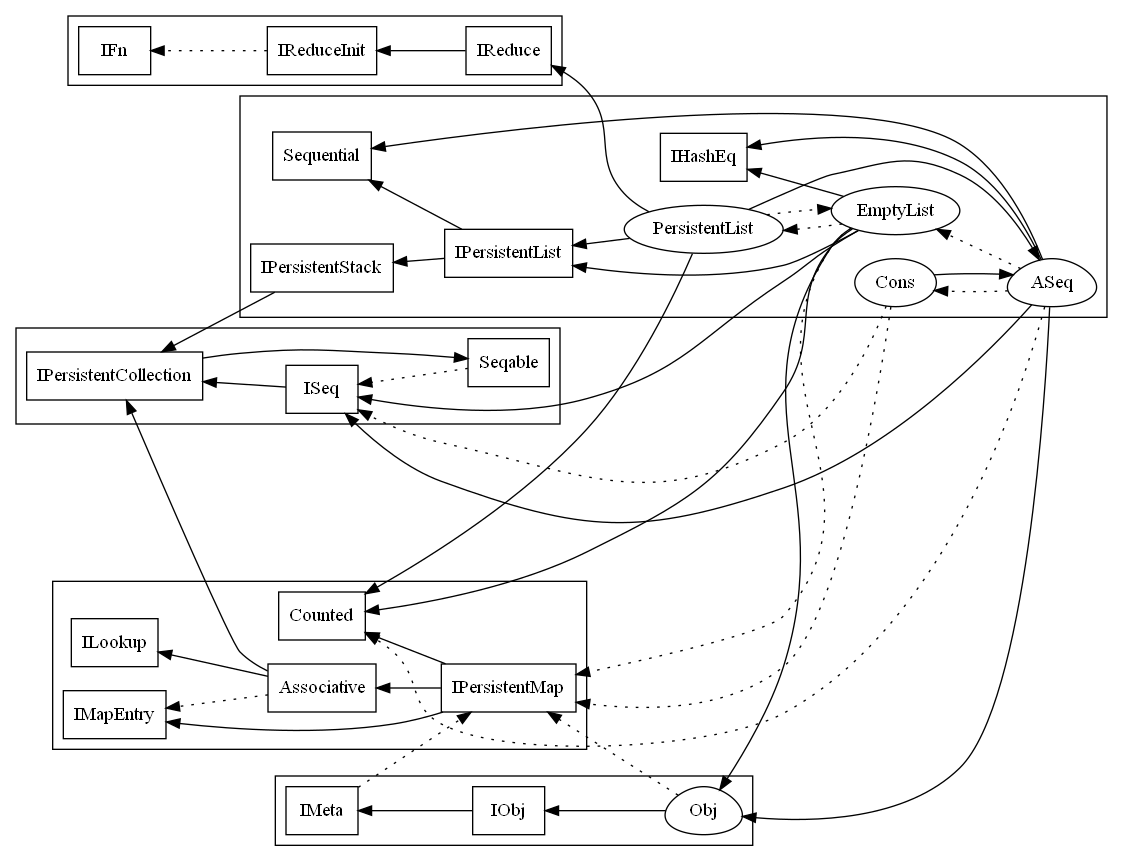
I have grouped to items to try to indicate how they can be broken into manageable pieces. Where there is true circularity, we cannot develop the items independently.
The first such grouping is the trio of Seqable, IPersistentCollection, and ISeq; mutually recursive definitions are required. Let’s look at these interfaces in detail.
type [<AllowNullLiteral>] Seqable =
abstract seq : unit -> ISeq
and [<AllowNullLiteral>] IPersistentCollection =
inherit Seqable
abstract count : unit -> int
abstract cons: obj -> IPersistentCollection
abstract empty: unit -> IPersistentCollection
abstract equiv: obj -> bool
and [<AllowNullLiteral>] ISeq =
inherit IPersistentCollection
abstract first : unit -> obj
abstract next : unit -> ISeq
abstract more : unit -> ISeq
abstract cons : obj -> ISeq
The [AllowNullLiteral] attributes will occur on many of our interface declarations. null is definitely a first-class citizen in Clojure. For example, a null return from Sequable.seq() is an empty-sequence/end-of-sequence indicator; thus we must allow null values for ISeq.
With these three in hand, the remaining interfaces needed for a basic Cons can be defined directly with no mutual recursion, just the appropriate ordering to respect inheritance.
The second area of possible mutual recursion involves Cons and ASeq. ASeq is an abstract class that provides default implementations for a number of interface methods.
It is ubiquitous. A quick count shows 22 classes in the C# code for Clojure having ASeq as their base class.
One default provided by ASeq is for the cons method, that adds an item to the front of a sequence. The default implentation – no surprise – creates a Cons. However, we woulld Cons to be based on ASeq to pick up the defaults ASeq provides. We could break the cycle by defining Cons without reference to ASeq, breaking the cycle at the expense of duplicating the defaults. I’ll go with the mutual recursion.
Finally, we see a circularity between EmptyList and PersistentList. PersistentList uses EmptyList as the return value for IPersistentCollection.empty(). EmptyList returns a PersistentList for IPersistentCollection.cons(o) and ISeq.cons(o). As Clojure has defined it, a PersistentList must have at least one element; an EmptyList obviously has none. Why not return a Cons for cons()? There is a bias in a few places in the runtime code, notably RT.conj and RT.cons to return a PersistentList of one element rather than a Cons of that element with null. (Continuing to conj/cons/etc. onto the former leads to more efficiency.) Alternatively, we could allow PersistentList to have
The embrace between PersistentList and EmptyList can be handled by mutually recursive definitions. The alternative of using a discriminated union for the pairing loses the ability to inherit from ASeq – that would cause a lot of code duplication.
Two other areas of the map to examine are the IMeta/IObj/Obj triple and the IFn/IReduceInit/IReduce triple. The former comes into play because most collections support attachment of metadata in the form of an IPersistentMap instance. However, the metadata-related code does not involve creating any persistent maps, just passing them around, so we can build the code without introducing any relationships to concrete map classes.
The reduce functionality brings IFn into the mix. This opens up a lot of complexity. Eventually we will have to implement the abstract classes that support IFn functionality. Fortunately, that does not appear to create any circularities. Some of the collections, such as LazySeq also require IFn
We’re getting a little too deep here. Let’s look at the minimum required to get our Cons implemented in the style of Clojure:
- Define the interfaces shown above, with the only mutual recursion being among
Seqable+IPersistentCollection+ISeq. - Implement
Obj. - Implement
EmptyList. If we makeconsand raise errors to get started, we can isolate this to test. - Implement
Cons,ASeqtogether. - Implement
PersistentList, mutually recursive withEmptyList. Finish the definition ofEmptyList.cons. - Test it all.
The good news
Feeling the burn? The good news is that this is probably the nastiest bit of analysis we have to do on the data structure side. we can illustrate all this with a ‘simple’ implementation of Cons that pulls together all these pieces. With that under our belts, when we implement more complicated data structures, such as hash array mapped tries with persistence, we can focus on the inherit complexity of the data structure itself; slotting it into the ecosystem will be an easy task.
Even better news
We’ll take the time in the next few posts to show how to implement simple versions of some collections types – cons cells, maps, etc. – before approaching this whole mess in gory detail.